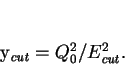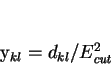|
|



Next: Jet resolution variables
Up: The algorithm
Previous: The exclusive mode
Subjet analysis and  mode mode
Once the hadronic final state has been decomposed into jets, the
structure of the jets themselves can be investigated. This is commonly
known as a subjet analysis. The procedure is physically (and
practically) identical to that employed in the analysis of an  event. In the
event. In the 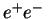 case, all final state objects are used as input to
the algorithm. In a subjet analysis on a particular jet, only the
particles within that jet are used as input. The steps are as follows; case, all final state objects are used as input to
the algorithm. In a subjet analysis on a particular jet, only the
particles within that jet are used as input. The steps are as follows;
- Define a resolution parameter
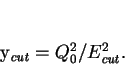 |
(4) |
The parameter
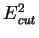 may be chosen by the user, but is
conventionally taken to be the square of the total energy of the may be chosen by the user, but is
conventionally taken to be the square of the total energy of the 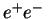 event
(or the event
(or the 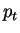 of the jet) in the frame in which the algorithm is run. These are the
default settings in KtJet. of the jet) in the frame in which the algorithm is run. These are the
default settings in KtJet.
- For each pair of objects
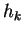 and and 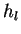 , construct the rescaled
resolution variable , construct the rescaled
resolution variable 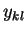
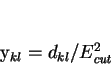 |
(5) |
where 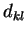 is defined as in section 2.1. is defined as in section 2.1.
- Find
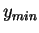 , the smallest of the , the smallest of the 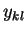 . If . If
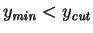 , , 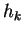 and
and 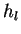 are combined into a single object with momentum are combined into a single object with momentum 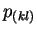 according to a user specified recombination scheme (parameter
recom).
according to a user specified recombination scheme (parameter
recom).
- Repeat the procedure until all pairs of objects have
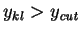 . The remaining objects are called subjets. . The remaining objects are called subjets.
As described in section 2.2, one can choose to stop merging when
a given number of jets is reached, instead of specifying the stopping scale
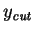 . .



Next: Jet resolution variables
Up: The algorithm
Previous: The exclusive mode
Jonathan Couchman
2002-10-02
|