|
|



Next: KtLorentzVector Methods
Up: KtEvent methods
Previous: KtEvent methods
Monotonicity
Although in practice most users will not have to face the issue, it is
worth bearing in mind that recombination schemes 1 to 5 are not
guaranteed to lead to monotonic resolution variables, i.e. it is NOT
necessarily true that
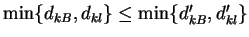 , where , where 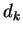 and and 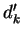 are the
resolution variables before and after recombination respectively. This
means that, physically, the question ``How many jets are there at a
particular scale are the
resolution variables before and after recombination respectively. This
means that, physically, the question ``How many jets are there at a
particular scale 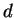 ?'' may not have a unique answer. In KtJet, as
should be clear from section 2.2, for a particular value
of ?'' may not have a unique answer. In KtJet, as
should be clear from section 2.2, for a particular value
of
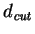 set by findJetsD, the largest value of set by findJetsD, the largest value of 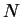 (i.e.
the first place at which (i.e.
the first place at which
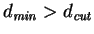 ) will be returned by
getNJets. Similarly, there may be no value of ) will be returned by
getNJets. Similarly, there may be no value of
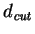 for
which a particular event has for
which a particular event has 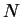 jets. There will however always be a jets. There will however always be a
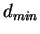 value at which the event changed from value at which the event changed from 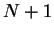 to to 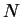 jets,
which is the value returned by getDMerge. The above
discussion also applies to the jets,
which is the value returned by getDMerge. The above
discussion also applies to the 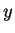 variables and associated methods. variables and associated methods.
Jonathan Couchman
2002-10-02
|