ktjet is hosted by Hepforge, IPPP Durham
next up previous
Next: The scheme, recom=3 Up: Recombination schemes Previous: The scheme, recom=1


The $p_t$ scheme, recom=2


$\displaystyle p_{t(kl)}$ $\textstyle =$ $\displaystyle p_{tk}+p_{tl},$  
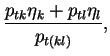$\displaystyle \eta_{kl}$ $\textstyle =$ $\displaystyle \frac{p_{tk}\eta_k+p_{tl}\eta_l}{p_{t(kl)}},$  
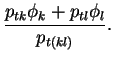$\displaystyle \phi_{kl}$ $\textstyle =$ $\displaystyle \frac{p_{tk}\phi_k+p_{tl}\phi_l}{p_{t(kl)}}.$ (11)

This definition constrains only the 3 spatial components of the object's 4-vector. The combined object is made massless by setting its energy equal to the magnitude of its 3-momentum. If massive objects are input (for instance particle 4-vectors from a simulated event) they are made massless in the same way before the $d_{kB}$ and $d_{kl}$ are calculated. Compare the $E_t$ scheme (section 2.5.4).
Jonathan Couchman 2002-10-02