ktjet is hosted by Hepforge, IPPP Durham
next up previous
Next: The scheme, recom=4 Up: Recombination schemes Previous: The scheme, recom=2

The $p_t^2$ scheme, recom=3


$\displaystyle p_{t(kl)}$ $\textstyle =$ $\displaystyle p_{tk}+p_{tl},$  
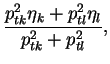$\displaystyle \eta_{kl}$ $\textstyle =$ $\displaystyle \frac{p^2_{tk}\eta_k+p^2_{tl}\eta_l}{p^2_{tk}+p^2_{tl}},$  
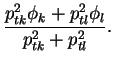$\displaystyle \phi_{kl}$ $\textstyle =$ $\displaystyle \frac{p^2_{tk}\phi_k+p^2_{tl}\phi_l}{p^2_{tk}+p^2_{tl}}.$ (12)

This definition constrains only the 3 spatial components of the object's 4-vector. The energy is made equal to to the magnitude of its 3-momentum, thus making the combined object massless. Note also that this definition of the $p_t^2$ scheme is that used in the Fortran implementation of the algorithm [2]. It is not equivalent to the monotonic $p_t^2$ scheme defined in equations 16 and 17 of reference [1]. We discuss the issue of monotonicity further in section 3.1.1.
Jonathan Couchman 2002-10-02